Differenciálegyenletek megoldása Monte Carlo módszerrel

Konzulens:

Dr. Vaitkus Márton

Tárgy:

Önálló laboratórium 1 - Egészségügyi mérnök, MSc Eü.
Önálló laboratórium 2 - Egészségügyi mérnök, MSc Eü.
Önálló laboratórium 1 - Irányító és látórendszerek MSc. főspec.
Önálló laboratórium 1 - Vizuális informatika MSc. főspec.
Önálló laboratórium 2 - Irányító és látórendszerek MSc. főspec.
Önálló laboratórium 2 - Vizuális informatika MSc. főspec.
Önálló laboratórium - Szoftverfejlesztés és rendszertervezés specializáció, BSc Info.
Önálló laboratórium - Irányítórendszerek ágazat, BSc Vill.

Hallgatói létszám:

Folytatás:

Szakdolgozat / Diplomaterv
PhD
TDK dolgozat

Leírás:

Forrás: Grid-Free Monte Carlo for PDEs with Spatially Varying Coefficients

A mérnöki tudományokban és a grafikában is gyakran szükséges differenciálegyenletek közelítő megoldása egy tartomány felett: pl. valamilyen mennyiség (pl. hőmérséklet, vagy RGB szín) legegyenletesebb eloszlását a térben az ún. Laplace-egyenlet megoldásával számíthatjuk ki. A klasszikus numerikus módszerek (pl. végeselem-módszer) használatához diszkrét elemekre kell bontani a tartományt (pl. háromszögekkel), ami a gyakorlatban számos nehézséggel jár.

Forrás: https://www.cs.cmu.edu/~kmcrane/Projects/MonteCarloGeometryProcessing/index.html

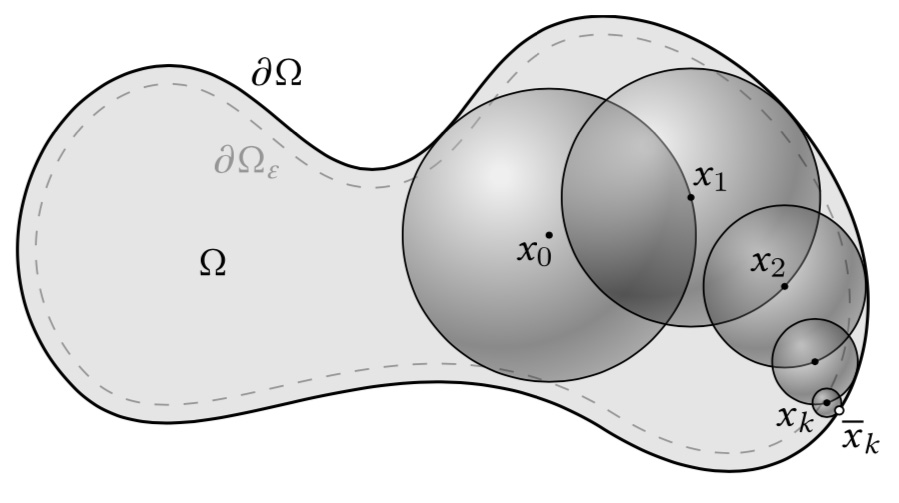
Egy alternatív megközelítés [1] a sugárkövetés-alapú képszintézisben széles körben használt Monte Carlo módszert [2] általánosítja az ilyen problémák megoldására. Az egyes pontokból véletlen irányokban sétákat indítunk a tartomány határáig, és a határon adott értékeket megfelelően átlagoljuk. A tartomány határa bármilyen reprezentációban adott lehet, amitől távolságot tudunk becsülni: pontfelhő, mesh, vagy akár implicit távolságmező. A módszer előnye, hogy nem igényli a térfogat mesterséges elemekre bontását, a megoldás pontossága tetszés szerint hangolható és az algoritmus párhuzamosítása magától értetődő. A módszer implementációja is igen egyszerű.

Forrás: https://www.cs.cmu.edu/~kmcrane/Projects/MonteCarloGeometryProcessing/index.html

A hallgató feladatai:

Tanulmányozza az [1] cikket és a kapcsolódó előadásokat.
Készítsen programot, ami képes Laplace egyenletek megoldására Monte Carlo módszerrel 2D és 3D tartományok felett.
Vizsgálja meg az algoritmus GPU-alapú implementációjának lehetőségeit. [3]

Ajánlott irodalom:

[1] Shawney, R., Crane, K.: Monte Carlo Geometry Processing. ACM Transactions on Graphics, Vol. 39(4), 2020.

[2] Szirmay-Kalos, L.: Globális illuminációs módszerek (előadási jegyzet). http://cg.iit.bme.hu/portal/oktatott-targyak/szamitogepes-grafika-es-kepfeldolgozas/globalis-illuminacios-modszerek

[3] Mossberg, L.: GPU-Accelerated Monte Carlo Geometry Processing for Gradient-Domain Methods. Linköping University.