3D geometriai modellezés OpenVDB alapon

Konzulens:

Dr. Vaitkus Márton

Tárgy:

Önálló laboratórium 1 - Egészségügyi mérnök, MSc Eü.
Önálló laboratórium 2 - Egészségügyi mérnök, MSc Eü.
Önálló laboratórium 1 - Irányító és látórendszerek MSc. főspec.
Önálló laboratórium 1 - Vizuális informatika MSc. főspec.
Önálló laboratórium 2 - Irányító és látórendszerek MSc. főspec.
Önálló laboratórium 2 - Vizuális informatika MSc. főspec.
Önálló laboratórium - Szoftverfejlesztés és rendszertervezés specializáció, BSc Info.
Önálló laboratórium - Irányítórendszerek ágazat, BSc Vill.

Hallgatói létszám:

Folytatás:

Szakdolgozat / Diplomaterv
PhD
TDK dolgozat

Leírás:

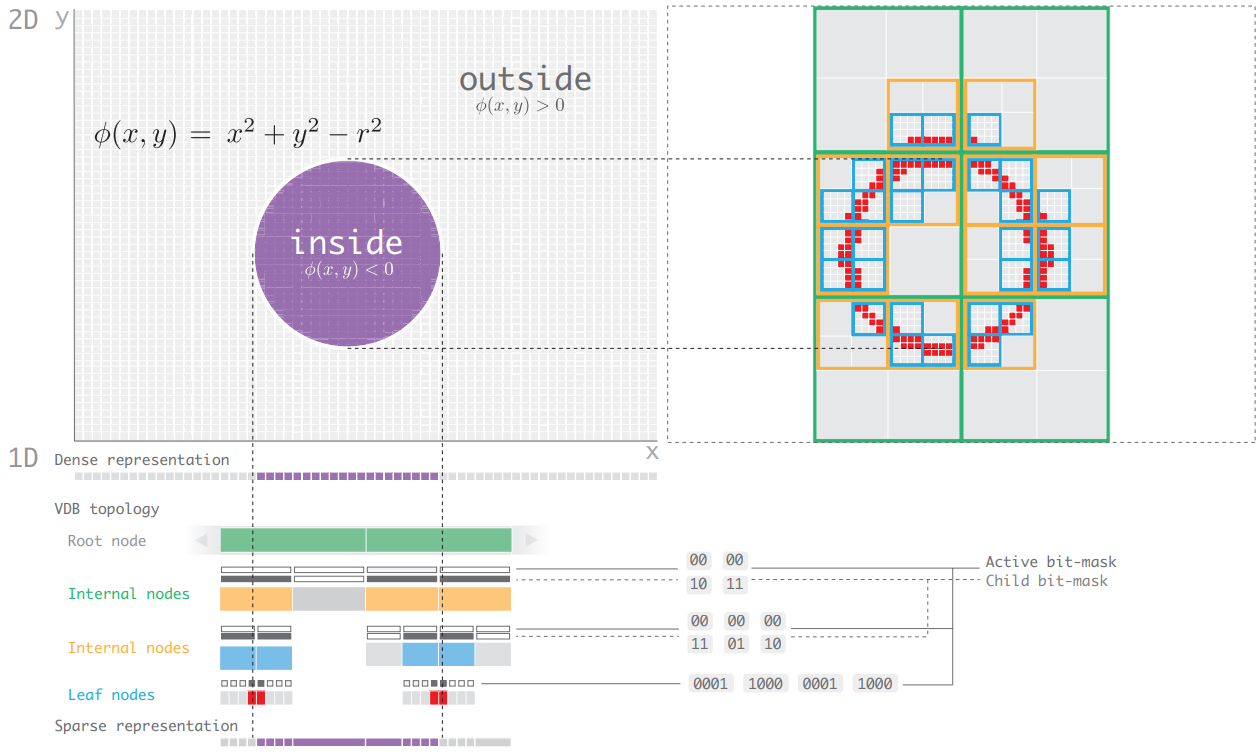
A 3D objektumok modellezésének egy lehetséges módszere hogy határfelületet implicit módon, azaz valamilyen skalárfüggvény F(x,y,z) = 0 szintfelületeként definiáljuk, aminek számos előnye van: pl. könnyen lehet halmazműveleteket (unió, metszet, stb.) végezni, vagy sugárkövetni. Míg egyszerűbb primitív alakzatokat (pl. sík, vagy gömb) meg lehet adni implicit képlettel, általában ez már nem lehetséges, hanem valamilyen diszkrét, mintavételezett formában kell tárolnunk egy 3D skalármezőt. A szabályos rács 3D tér felett igen költséges és az olyan klasszikus adaptív adatszerkezetek, mint pl. az oktális fa (octtree) sem mindig használhatóak ha nagy és részletes modellt szeretnénk tárolni.

A vizuális effektek (VFX) területén a térfogati adatok tárolására az ipari standard a VDB, ami egy fix mélységű fa használatával konstans időben(!) olvasható, írható, bővíthető térfogati adatszerkezet. A nyílt forráskódú OpenVDB könyvtár ma már szinte minden VFX szoftver integráns részét képezi és számos hasznos funkciót (pl. halmazműveleteket, távolságmező számítást, stb.) implementál, így vélhetően jól használható lehetne implicit felületekkel történő geometriai modellezésre is.

Szükséges előismeretek:

grafika alapjai, C++ programozás

A hallgató feladatai:

1. Ismerkedjen meg az OpenVDB könytárral.

2. Implementáljon 3D grafikus tesztkörnyezetet, ami képes implicit felületmodellezésre pl. primitív elemek halmazműveletekkel való kombinációjával.

3. Vizsgálja meg szabadformájú felületek (pl. mesh-ek) implicit modellezésének lehetőségeit és/vagy a GPU-alapú NanoVDB könyvtárat.

Ajánlott irodalom:

[1] Museth, K.: VDB: High-Resolution Sparse Volumes with Dynamic Topology. SIGGRAPH 2013. - YouTube.

[2] Kambampati et al.: Geometry Design Using Function Representation on a Sparse Hierarchical Data Structure. CAD, 2021.